A metronome spin stabilizes time-crystalline dynamics
New paper published by Niklas Euler and Adrian Braemer
An illustration of the two-step Floquet cycle of the one-dimensional (1D) system considered in this work.
Published:
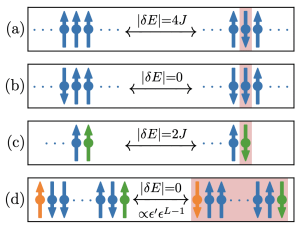
A visual summary of the different spin-flipping processes and their associated energy differences. The spins in the bulk are colored blue, whereas the metronome is colored orange, and the right edge spin is colored green. Flipped spins are highlighted with a red background.
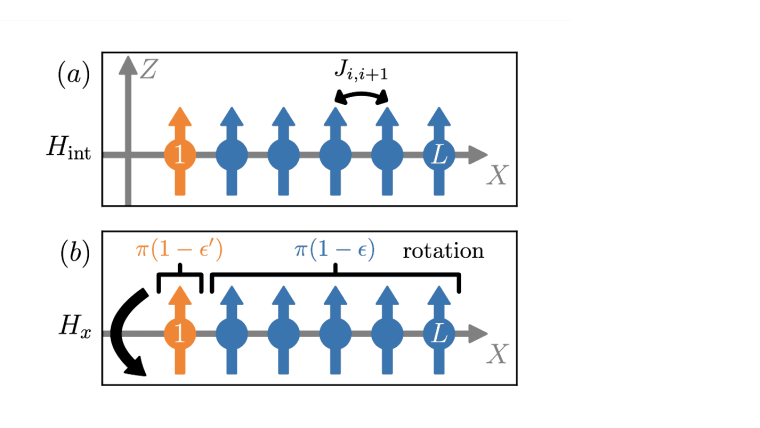
Image: Niklas Euler, Adrian Braemer, Luca Benn, Martin GärttnerIn the paper, a disordered quantum Ising chain subject to a time-periodic drive that rotates each spin by an angle π(1-εi) is investigated. When all spins undergo the same deviation ε and the system is initialized in a fully polarized state, the dynamics is known to be time-crystalline: the magnetization of the system exhibits periodically doubled oscillations for time scales that grow exponentially with the length of the chain. In this work, the effect of a deviation ε that differs between spins is investigated. It is found that a reduction of ε for a single spin drastically increases the lifetime of the spatio-temporal order, suggesting the name “metronome” spin. Using perturbative arguments in an average Hamiltonian, this observation is explained for initial states with macroscopic bulk magnetization. Moreover, in the case of random bitstring initial states, the increase in the lifetime of a topological edge mode, which can also be understood in the same picture, is reported. Finally, a modified geometry in which the metronome spin is not directly part of the chain, which affects the dynamics in the two considered scenarios in different ways, is discussed. Our results reveal the complicated dynamics that occur in Floquet systems under the influence of a spatially varying drive, opening new avenues for Floquet engineering.