Semiclassical method for simulating quantum spin systems
Adrian Braemer, Javad Vahedi and Martin Gärttner publish new paper
A schematic of the discrete cluster truncated Wigner approximation.
Published:
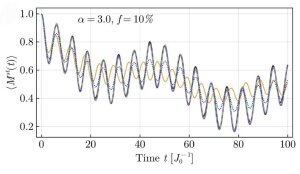
The panels show results for longrange interactions with α = 1.0
Image: Adrian Braemer, Javad Vahedi and Martin GärttnerThis paper investigates the application of the truncated Wigner approximation to spatially disordered quantum spin systems.
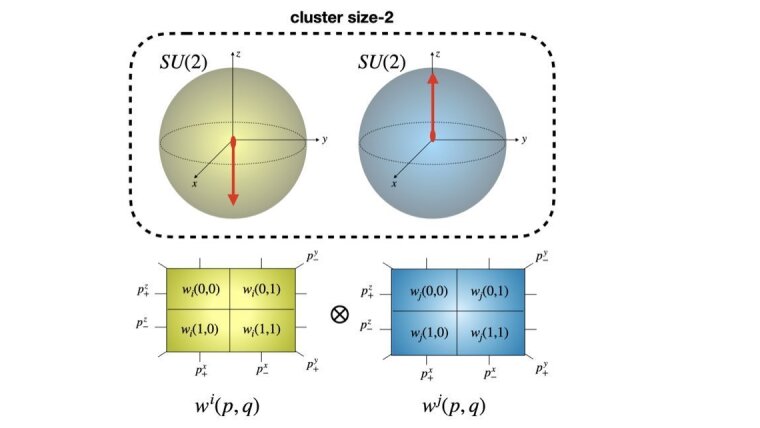
This numerical method, based on a semiclassical approximation of quantum dynamics in phase space formulation, enables the solution of large spin systems comprising hundreds to thousands of spins. In its basic form, each spin is assigned three classical degrees of freedom, and all interactions between the spins are approximated. However, this straightforward approach fails in strongly interacting systems. To address this, multiple spins are first grouped into clusters, and then a larger number of classical degrees of freedom is assigned to each cluster. The main focus of this paper is comparing various clustering strategies. It is shown that, due to spatial disorder, the system essentially breaks down into pairs of spins (i.e., clusters of size two). This specific clustering strategy allows the system's dynamics to be reproduced almost exactly under strong disorder, and even under weak disorder, the results are significantly better than those obtained with other clustering strategies.