Nonlinear dynamics of polaritons

Prof. Dr. Ulf Peschel

Nonlinear optics in periodic photonic structures

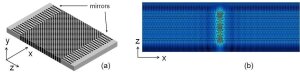
Here we focus on intensive numerical and analytical studies of the light dynamics inside artificial photonic structures endowed with a non-resonant optical nonlinearity (cubic or quadratic). A complete photonic device can be implemented "on-chip" at micrometer scale inside an appropriately patterned photonic crystal slab. An example is an all-photonic crystal resonator made of a high-index material (like GaAs) with an instantaneous Kerr-nonlinearity (see Fig. a). This "on-chip" device shows an optical bistability and can be considered as an essential building block of any logical operation. Due to nonlinear self-collimation the light focuses into a narrow region forming a robust localized object with well-defined shape and power, also called dissipative soliton. This robust localized object can be switched on and off and even shifted at any position along the device at will (Fig. b).

The photonic crystal changes the diffraction properties of light reducing drastically the size of dissipative solitons, and as a consequence the operation power of the device. This can be exploited for the purpose of fast low-power all-optical switching with a potential switching frequency of several hundreds of GHz.

Nonlinear optics in the regime of strong light-matter coupling

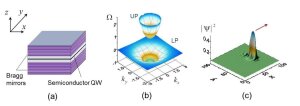
Here we study the nonlinear dynamics of light trapped in a tiny volume of micro-resonators, close and even beyond the diffraction limit. The light strongly interacts with the host material, creating significant nonlinear and quantum electrodynamics effects. An example is a planar microresonator with embedded semiconductor quantum wells (see Fig. a). The striking change of optical properties occurs when the conditions for the strong light-matter coupling regime inside a resonator are fulfilled. Under such conditions, the elementary excitations of the system can no longer be described as barely photonic, but rather as hybrid radiation-matter states, i.e. light and matter entangle and form a new quasi-particle called exciton-polariton. In the linear limit they exhibit a dispersion relation with two branches, called lower- (LP) and upper-(UP) polariton branches, separated by a gap (Rabi splitting) (see Fig. b). The new physics of this system originates from the half-light half-matter nature of polaritons. They are characterized by a strong nonlinearity and fast relaxation dynamics.

An important feature of the strong light-matter interaction is that strength and sign of the polariton dispersion can be controlled by changing the transverse momentum by means of inclination of the pump beam (see Fig. b). It leads to new degrees of freedom for the control of light. For instance, this makes possible the realization of very effective parametrical four- wave mixing processes or the formation of robust localized states moving with a given velocity in the plane of the cavity (see Fig. c).