Konstruktion der Quantenraumzeit: Spin-Schaum-Modelle und die Renormierungsgruppe
Eine offene Fragestellung in der theoretischen Physik ist die Beschreibung des Zusammenspiels von Materie und dynamischer Raumzeit auf kleinsten Skalen. Auf der einen Seite steht die Materie, beschrieben durch Quantenfeldtheorien, auf der anderen Seite die deterministische, geometrische Beschreibung der Raumzeit durch die Allgemeine Relativitätstheorie. Diese Beschreibungen sind inkompatibel, denn u.a. setzt eine Quantenfeldtheorie einen fixierte Hintergrundsraumzeit voraus. Darüber hinaus wissen wir, dass auf kurzen Skalen, d.h. hohen Energien, die klassische Beschreibung der Raumzeit zusammenbricht, Singularitäten auftreten und die fundamentale Quantennatur der Materie nicht ignoriert werden kann. Die Erwartung ist, dass diese offenen Fragen durch eine Theorie der Quantengravitation gelöst werden.
Der Weg zu einer solchen Theorie ist nicht eindeutig, und als Konsequenz existieren viele verschiedene Ansätze. Einiger dieser Ansätze machen die wichtige Annahme ist die sogenannte Hintergrundsunabhängigkeit. Die Allgemeine Relativitätstheorie beschreibt die Raumzeit als dynamische Geometrie. Deshalb ist keine Raumzeit ausgezeichnet oder bevorzugt, so dass es unphysikalisch ist einen Hintergrund zu fixieren. Zwei populäre Ansätze die auf diesem Prinzip aufbauen sind die Spin-Schaum-Quantengravitation und die verwandte kanonische Schleifen-Quantengravitation.
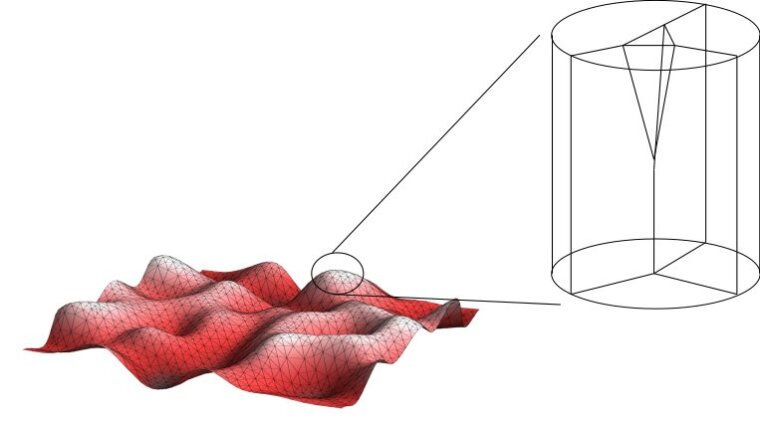
Spin-Schaum-Modelle sind Pfadintegralansaetze der Quantengravitation und koennen als generalisierte Gittereichtheorien verstanden werden. Die Idee ist, dass die Raumzeit ersetzt wird durch eine Quantensuperposition von Raumzeiten. Dazu wird über alle möglichen Raumzeiten summiert, gewichtet mit einer Quantenamplitude. Analog zu Gittertheorien fuehrt man dazu ein Gitter / eine Diskretisierung ein und summiert über diskrete "Bausteine der Raumzeit". Einer der Haupterfolge der Theorie ist die Herleitung des semi-klassischen Limes eines solches Bausteins, der verwandt ist mit dem Regge Kalkül, einer diskreten Formulierung der Gravitation.
Die Emmy Noether Nachwuchsgruppe beschäftigt sich mit drei eng verknüpften Schlüsselfragen der Spin-Schaum-Quantengravitation. Die Dynamik und die Renormierungsgruppe der Theorie, Berechenbarkeit und numerische Methoden und Observablen und Materiekopplung an Spin-Schaum-Modelle
Renormierungsgruppe und Phasendiagramm
Wie können wir Kontakt mit beobachtbarer Physik herstellen? Welchen Einfluss hat die Diskretisierung und wie können wir einen Kontinuumslimes definieren? Gibt es unterschiedliche Phasen mit unterschiedlichen Eigenschaften? Die Renormierungsgruppe (oder "coarse graining") ist das entscheidende Werkzeug um diese Fragen zu untersuchen, indem man Theorien auf verschiedenen Gittern in Relation zueinander setzt.
Berechenbarkeit der Theorie und numerische Methoden
Berechnungen in Spin-Schaum-Modellen erfordern generell numerische Methoden, z.B. um Spin-Schaum-Amplituden zu berechnen oder für die Renormierung jener Amplituden (Tensor-Netzwerk-Renormierung oder Monte Carlo Methoden). Darüber hinaus suchen wir nach neuen numerischen Methoden, die die Berechenbarkeit von Spin-Schaum-Modellen erleichtern.
Observablen und Materie
Um die Eigenschaften der Quantenraumzeit zu verstehen sind Observablen unabdingbar. Einerseits sind dies geometrische Observablen wie die spektrale Dimension oder Krümmung. Andererseits ist beschreiben Spin-Schaum-Modelle nur pure Gravitation, so dass es unabdingbar ist zusätzlich Materie an die Quantenraumzeit zu koppeln.