Semiklassische Methode zur Simulation von Quantenspinsystemen
Adrian Braemer, Javad Vahedi und Martin Gärttner neuste Publikation
A schematic of the discrete cluster truncated Wigner approximation.
Meldung vom:
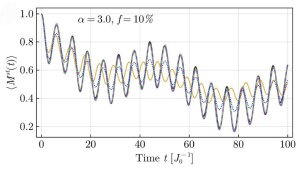
The panels show results for longrange interactions with α = 1.0
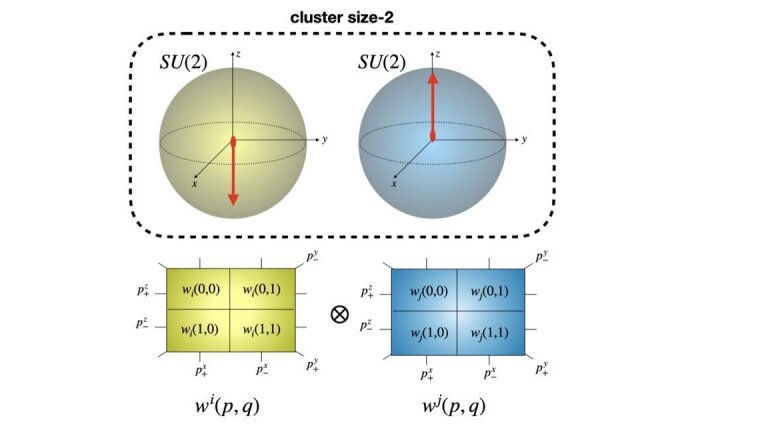
Foto: Adrian Braemer, Javad Vahedi and Martin GärttnerIn diesem Paper wird die Anwendung der Truncated-Wigner-Approximation in räumlich ungeordneten Quantenspinsystemen untersucht.
Diese numerische Methode basiert auf einer semiklassischen Näherung der Quantendynamik in der Phasenraumformulierung und erlaubt das Lösen von großen Spinsystemen mit vielen hunderten bis tausenden Spins. In der Grundvariante werden jedem Spin 3 klassische Freiheitsgrade zugeordnet und die Interaktionen zwischen den Spin angenähert. Diese einfache Methode versagt allerdings in stark wechselwirkenden Systemen, sodass es nötig ist zuerst mehrere Spins zu einem Cluster zusammen zu schließen und dann diesem Cluster eine größere Anzahl an klassischen Freiheitsgraden zu zuordnen. Hauptgegenstand dieses Papers ist der Vergleich von verschiedenen Clusteringstrategien. Es wird gezeigt, dass durch die räumliche Unordnung, dass System im wesentlichen in Paare von Spins zerfällt (d.h. Cluster der Größe 2). Mit dieser speziellen Clusteringstrategie kann die Dynamik des System bei starker Unordnung fast exakt reproduziert werden und auch bei schwacher Unordnung sind die Resultate wesentlich besser als mit anderen Strategien.